The standard practice for sizing one's tank capacitor to one's neon-sign power supply transformer has always been to choose a cap value that resonates with the transformer secondary's inductance at the AC mains frequency (50/60 Hz). The reason given has been that this practice allows a maximum amount of power to be drawn from the transformer by having the reactances of the secondary L and capacitor C cancel each other out.

A question was raised on the pupman.com Tesla List asking whether this really was so. I decided to use Pspice to simulate operation of both static and sync rotary gaps and examine just what effects are caused by different size caps, and hopefully determine what really is the best size cap. Some surprising things were learned.

MicroSim Pspice V8.0 model

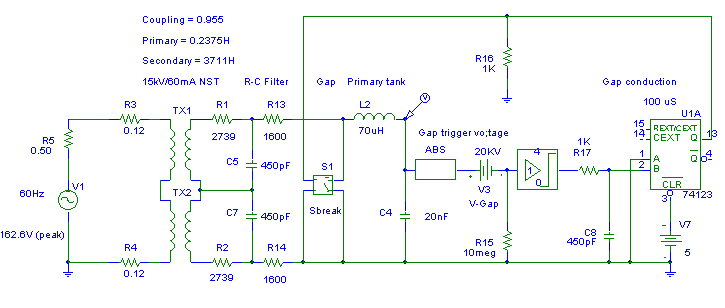
Above is the simulation schematic. The two transformers represent a single 15KV/60mA neon sign transformer and the model parameters were determined by Terry Fritz. R1-R4 are also part of the NST model. S1 is a voltage controlled switch and performs the function of the spark gap. C4 is the tank capacitor.

The stuff to the right of C4 triggers the "gap" after the tank cap reaches the breakdown voltage of the gap. The breakdown voltage is determined by DC voltage source V3, in series with the ABS absolute value operator. A unity-gain voltage limiter follows to trigger a 100 usec one-shot, and this pulse activates the gap switch.

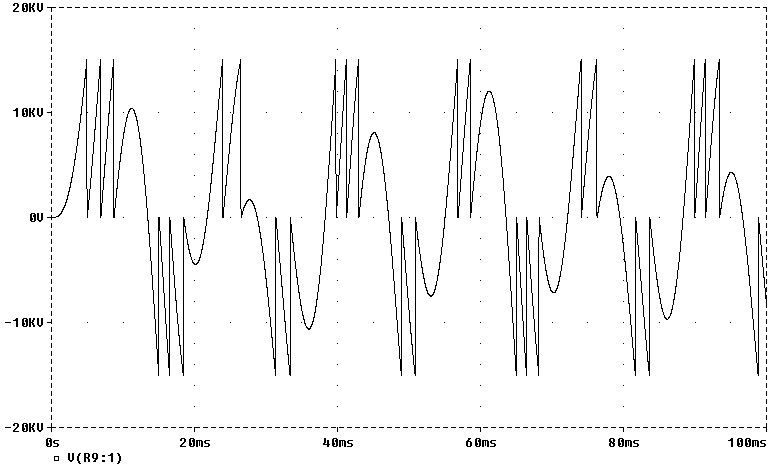
Above shows operation with a 10nF cap and 15KV static gap setting. There were 28 gap firings.

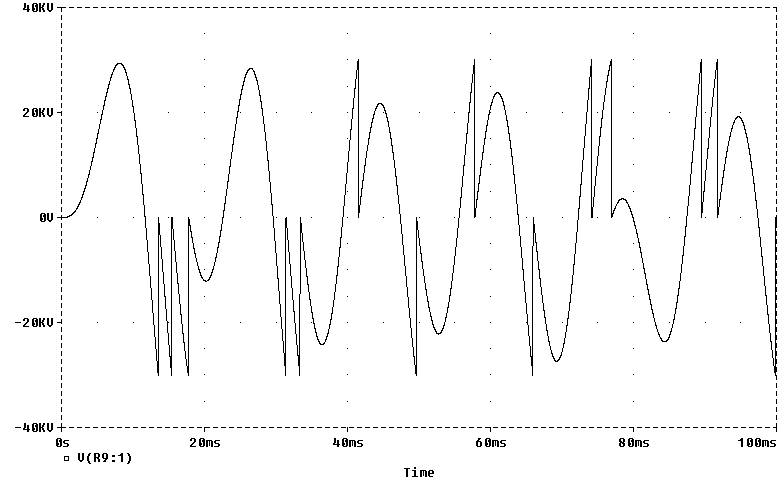
Above shows operation with a 10nF cap and 30KV static gap setting. There were 14 gap firings.

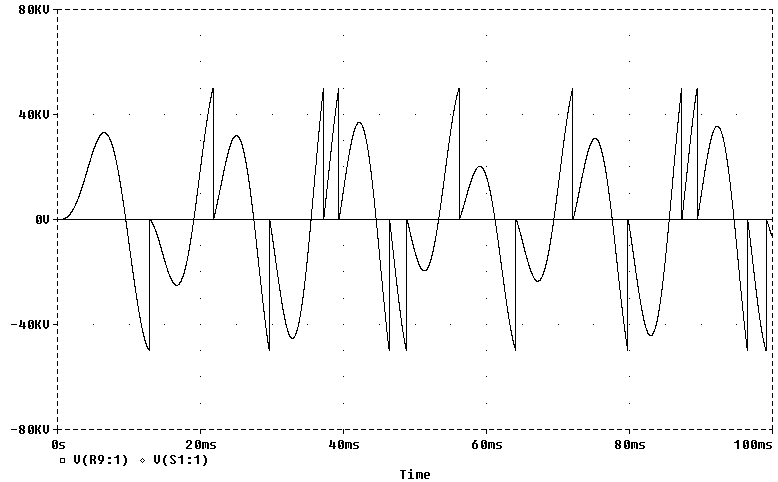
Above shows operation with a 4.5nF cap and a gap set for 50KV. Remember, this is just using a 15KV NST!!!

The tables below show the power delivered to the tank capacitor for various STATIC spark gap breakdown values and for capacitance values. As expected, the higher the gap breakdown voltage, i.e. the wider the gaps are spaced, the more power was delivered to the capacitor - a dangerous compromise. No effort was made to determine efficiency. I'm only interested in getting the maximum power into the arcs.

1. Static gap firings per 100msec simulation run, multiplied by 10.
2. Power = (1/2 C V**2) * gap firings per 1 second

Observations and conclusions:

1. For the given 15KV/60mA NST, there appear to be two optimum capacitance values which deliver maximum power through the capacitor: between 4-5nF and 8-9nF, neither one being the 10.8nF value required to achieve mains resonance.

2. Without exception, the higher the spark gap firing voltage (i.e. the wider one spaces the spark gap), the more power will be delivered to the capacitor, with comparably better performance. The obvious downside is that this places much higher stress and voltages on the transformer and capacitors. It is all too easy to get carried away with wider and wider gaps, giving one longer and longer arcs, until something blows.

3. Static gap firings are chaotic and will not ever settle down to a regular timing pattern. The goal of setting a static gap so that it fires once each half-cycle at the peak of the AC waveforms is an unattainable fantasy.

4. Estimating the required voltage value of one's capacitor based upon the transformer's voltage ratings is pointless, IMO. Using static gaps, the peak voltage has an upper limit imposed by the transformer and capacitor combination, and can be far in excess of 1.414 x NST RMS-Vrating. In the simulation examples above, using any capacitor less than 20nF with a 15KV NST allowed a 30KV gap to fire regularly. Spacing the gap even wider would have permitted even higher peak voltages, particularly with smaller-sized caps. Estimating the peak capacitor voltage at 1.414 times the NST faceplate voltage is wrong. The absolute upper limit of the peak voltage that the capacitor must withstand is mostly determined by the gap spacing. Now if only there were a definitive table relating gap spacing (at sea level) to breakdown voltage...

5. While it may appear that certain-valued smaller caps can process just as much power as larger ones (and thus be more economical), beware that the higher BPS firing rate that will necessarily occur with smaller caps will make them far more likely to fail.

I performed an experiment where I fed nominally 1volt AC from a variac into the NST primary and measured the secondary voltage with various capacitor values placed in parallel with the secondary. I calculated the secondary/primary voltage ratio (measuring both for each cap value), and compared this with the simulation model:

Except for the 10.6nF case, which happens to be the mains-resonant case, the results match extremely well. I believe the simulation results in the previous section are credible.

Recent discussions on the Pupman Tesla List now suggest that neon sign transformers exhibit a non-linear behavior when primary voltages are used near maximum and are used to charge capacitors. The result is that far greater currents than normal are passed through the NST's secondary (and primary), resulting in far greater power being processed. This is believed to be due to the NST's current shunts saturating, and somewhat circumvents their current limiting ability. This effect may be more pronounced when using larger than mains-resonant sized capacitors. While some suggest that caution be exercised so as not to burn out the NST, I think this is a godsend, and I finally have an explanation for the much hotter than expected operation of my protection resistors.

The simulations above do not take this behavior into account, so the optimal cap values suggested by these simulations may or may not be valid. Sorry to have dragged you through all of this only to tell you this now, but isn't that what makes coiling so interesting?

Back to Gary Lau's main Tesla Coil Page